Por Facundo Gola
El objetivo de este artículo es conocer el fenómeno de contacto entre la rueda y el riel, ya que es uno de los más característicos en la investigación dinámica ferroviaria debido a que es el principal condicionamiento de los sistemas ferroviarios, así como de sus limitaciones.
El contacto rueda riel ha sido ampliamente estudiado en el mundo de los ferrocarriles, debido a la importancia del mismo, a la hora de lograr tanto la prolongación de la vida útil de los sistemas de transporte, como la mejora y evolución de los mismos, tanto en mercancías como en las líneas de alta velocidad.
A lo largo del último siglo, se han desarrollado varias teorías con el objetivo de definir con la mayor precisión posible el contacto rueda riel. Partiendo del modelo Hertziano de contacto entre dos sólidos.
Para lo cual vamos a detenernos en el análisis de la compatibilidad entre rueda y riel mediante el parámetro de la huella de contacto en las siguientes situaciones:
- Teorías del contacto rueda riel
- Resolución analítica de la teoría de Hertz
El tipo de contacto entre material rodante y riel ferroviario da como resultado dos tipos de fuerzas que actúan en la zona de contacto, las fuerzas normales y las fuerzas tangenciales, resultantes de sistemas de pseudo deslizamiento que se originan en la zona de contacto, al darse simultáneamente los fenómenos de rodadura y fricción seca.
La carga vertical que soportan las ruedas es un factor a tener en cuenta, ya que de esta dependen otros factores como la fuerza de tracción máxima y la fuerza de adherencia máxima, esta última también depende del coeficiente de fricción existente entre las ruedas y los rieles, y por esto la adherencia supone una limitación del esfuerzo tractor.
Desde hace años se ha buscado incrementar la adherencia, sabiendo que el coeficiente de fricción que existe es relativamente pequeño. Actualmente, se puede considerar el total del peso como un factor adherente, y gracias a esto se consigue un aumento constante de la potencia.
Todas las teorías que estudian este tipo de contacto se basan en el estudio de dos cuerpos elásticos rodando uno sobre el otro, sometidos a cargas normales y tangenciales en la superficie de contacto. La zona de contacto entre la rueda y el riel se divide en dos:
- Zona de adherencia
- Zona de deslizamiento
Una de las primeras teorías que se desarrollaron acerca de la extensión de estas zonas en contacto rueda-riel, la propuso Carter en 1926, en la que supone que la zona de contacto es rectangular y uniforme, lateral al riel. Carter solo tiene en cuenta el pseudo deslizamiento longitudinal.
En 1958 Johnson amplía la teoría considerando la zona de contacto circunferencial y los pseudo deslizamientos longitudinal y lateral.
Más adelante, en 1964, junto con Vermeulen consideraron la superficie de contacto elíptica.
En 1963 y 1964 se desarrolla la Teoría de franjas cuyos autores son Haines, Ollerton y Halling, esta teoría solo es aplicables cuando hay pseudo deslizamiento longitudinal puro. Consiste en dividir la zona de contacto en franjas paralelas a la dirección de rodadura y en cada franja aplicaron la teoría de Carter. La solución que se obtenía en una de las franjas era independiente del resto. Esta teoría propone la forma correcta de las zonas de adhesión y deslizamiento.
En 1967 Kalker desarrolló otra teoría donde consideró que había una relación lineal entre las fuerzas de contacto tangencial y el pseudo deslizamiento.
Todas las teorías mencionadas toman como base la teoría de Hertz, que será explicada en este capítulo en mayor profundidad, y cuyas hipótesis permiten tratar la resolución de las fuerzas de contacto normales y tangenciales por separado.
En la teoría de Hertz se supone que las ruedas y el riel pueden considerarse como dos cuerpos en la que la superficie de contacto es esférica, si no se ejerciese presión sobre ninguno de los cuerpos, el contacto sería sencillamente un punto. Sin embargo, en el caso de la rueda y el carril ambos soportan cargas, esto hace que el contacto sea una elipse.
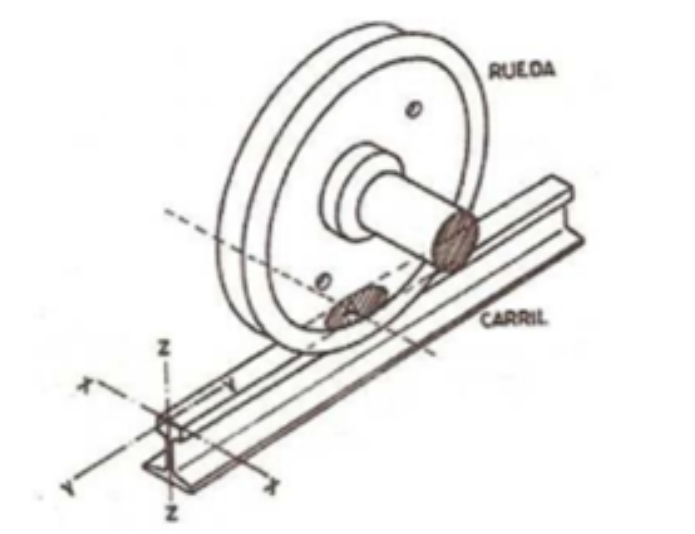
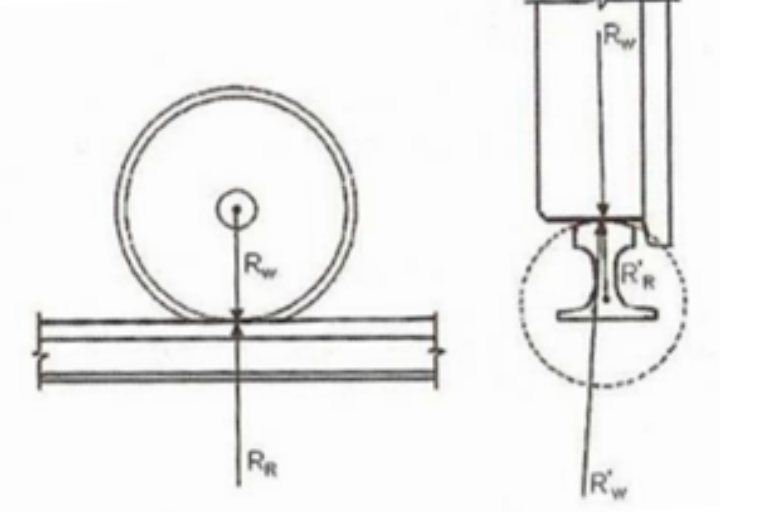
Uno de los principales objetivos de este artículo es obtener analíticamente las elipses de contacto rueda riel aplicando la teoría de Hertz, para distintos de niveles de carga aplicadas y así poder observar cómo varía la superficie de contacto.
Para ello se va a utilizar tablas de datos correspondientes a la Norme EN 13262, referentes a los tipos de acero de cada rueda, características mecánicas y geométricas.
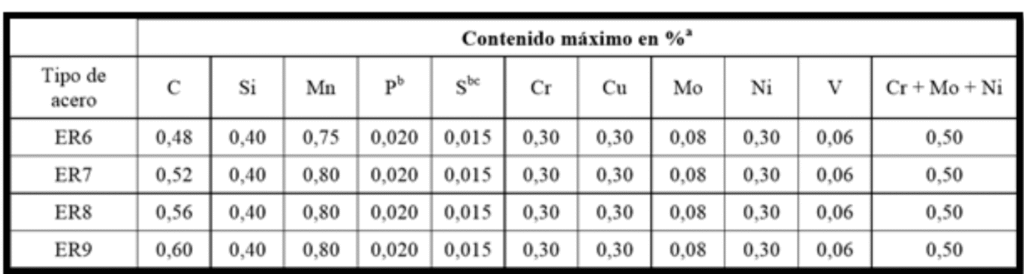
En la Tabla 1 correspondiente a la Norma EN 13262 se aprecian los porcentajes máximos de los diferentes elementos especificados:
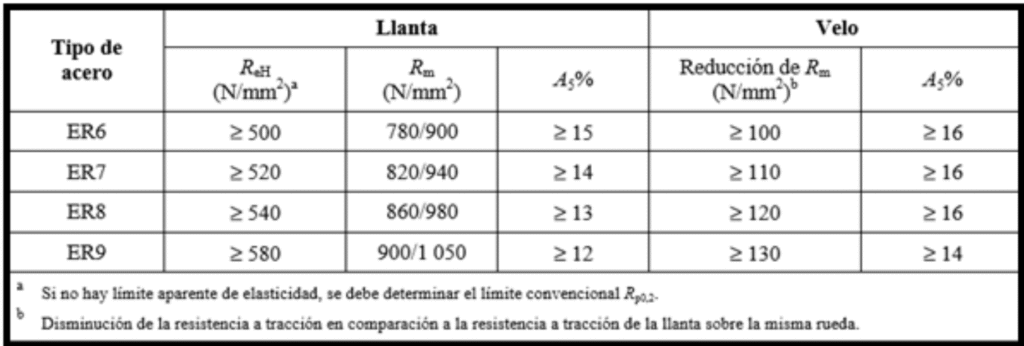
Posteriormente se detallan en Tabla 2 correspondiente a la Norma EN 13262 los valores correspondientes a características mecánicas, ensayos de tracción:
La norma EN 13262 en el ANEXO C.3 menciona que el Módulo de Elasticidad E teórico para todos los aceros es equivalente 210.000 MPa, y el coeficiente de Poisson es equivalente a 0,28, valores que vamos a utilizar más adelante al efectuar los cálculos:
E = 210.000 MPa
ⱱ = 0,28
Datos a considerar:
N = Fuerza normal total que actúa en la zona de contacto
R1 = Radio de rodadura principal de la rueda, en el punto de contacto
R2 = Radio de rodadura tangencial al riel, en el punto de contacto
ⱱ = Coeficiente de Poisson para la rueda y riel
E = Modulo de Elasticidad del Acero para el riel
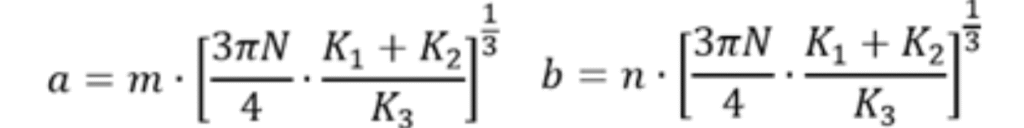
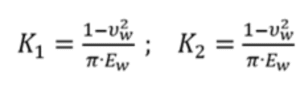
Para obtener m y n = Coeficiente depende del ángulo φ
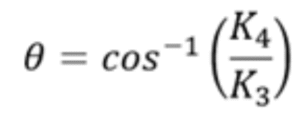
Se calcula K3 Constante geométrica de la Rueda y K4 Constante geométrica del Riel. Son variables dependientes de los radios de curvatura de las superficies en contacto
K3 = ½ x (1/R1 + 1/R1´) K4 = ½ x (1/R2´ + 1/R2)
Donde R1´es equivalente al radio de rodadura principal del Riel en el punto de contacto, igual a infinito = ∞.
Donde R2´es equivalente al radio de rodadura tangencial a la Rueda en el punto de contacto, igual a infinito = ∞.
K3 = ½ x (1/R1 + 1/R1´) K4 = ½ x (1/R2´ + 1/R2)
Posteriormente se calcula el valor de 𝜃, siendo el ángulo que forman los planos que contienen a los radios de curvatura de la rueda y el riel.
Cos 𝜃 = (K4-K3) / (K4+K3)
Ingresando con el valor de 𝜃 e interpolando en la Tabla 4 se calculan los valores de m y n, variables dependientes del ángulo entre los planos que contienen los radios de curvatura.
Los coeficientes m y n toman diferentes valores dependiendo del ángulo 𝜃:
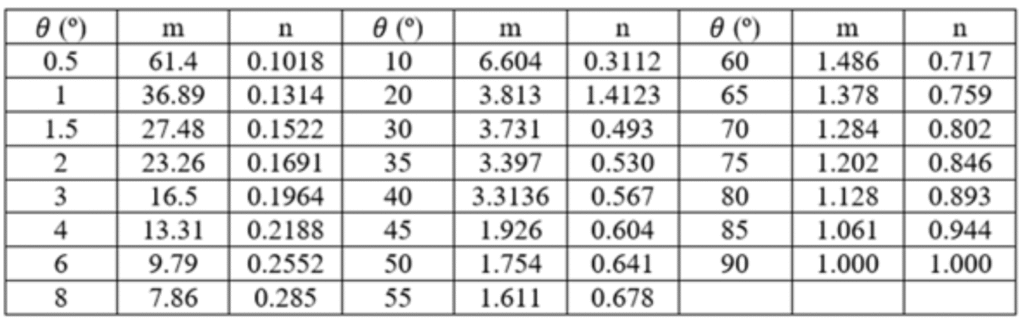
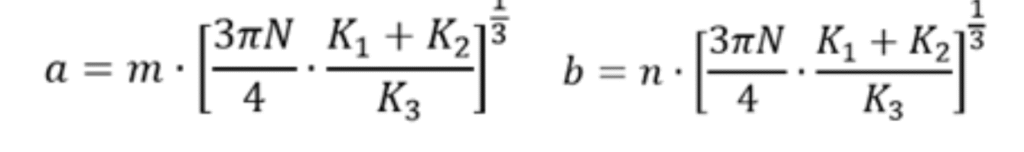
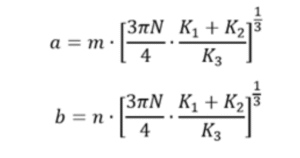
Considerando las fórmulas arriba detalladas, vamos a mantener el diámetro de rueda y riel constantes y se realizarán los cálculos para obtener la superficie de contacto para distintos valores de toneladas por eje (desde las 2tn hasta las 20 tn).
CONCLUSIONES
En base a los resultados y de acuerdo con cómo fueron variando los valores de los ejes a y b de la elipse de contacto, a medida que se modificaba el valor de la carga aplicada, podemos obtener las siguientes conclusiones:
En cuanto al área, cabe destacar la forma elíptica de la huella, con lo cual concuerda con la teoría de contacto propuesta por Hertz.
Los resultados arrojados demuestran que los valores referentes a la superficie de contacto aumentan a medida que la carga aplicada es mayor.
Existe una gran diferencia entre el área de contacto obtenida cuando la carga aplicada es de 2 tn y cuando es de 20 tn por eje, como se puede apreciar en la siguiente gráfica donde se relaciona el área de contacto (eje vertical) y la carga aplicada (eje horizontal).
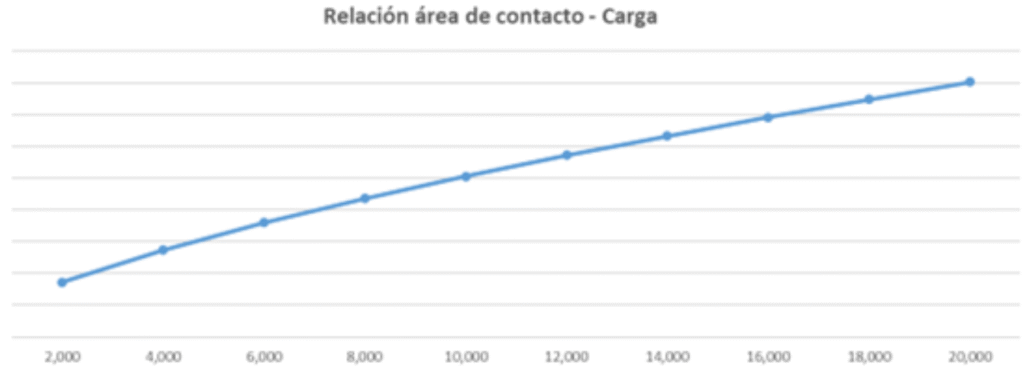
Por último, y como conclusión más relevante es mencionar que si bien hoy en día obviamente existen herramientas de software para realizar este tipo de análisis y estudiar el fenómeno del contacto rueda riel, es importante que tengamos presente que cada uno de nosotros, a los que nos gusta el maravilloso mundo de los ferrocarriles, con un poco de dedicación y utilizando las teorías y normas mencionadas podemos obtener los mismos resultados.
Facundo Gola
Ingeniero Mecánico y Profesor Universitario
Posgrados en Ingeniería Ferroviaria y Planificación del Transporte

